Overall pipeline

The image registration method implemented here was first described by Reddy and Chatterji [1]. The algorithm estimates the similarity transform (translation, rotation and scale) between two images.

The overall pipeline is shown below:

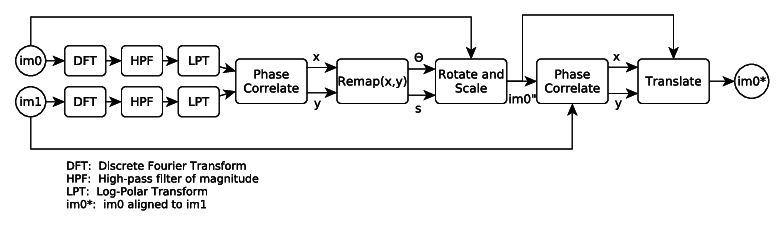
registration pipeline

Discrete Fourier Transform (DFT) to convert images into frequency domain
Smoothing and high-pass filter to avoid the “plus” artifact caused by borders and aliasing artifacts due to rotation
Log-polar transform to convert rotation and scaling in the Cartesian coordinate system to translations in the log-polar coordinate system
Phase Correlation to estimate the translation offset between two images

The first phase correlation block is used to estimate the rotation and scale difference between the two input images. This done after first representing the rotation and scaling as translations using the log-polar transform of the magnitude of the Fourier transforms of the images.

The first image is then rotated and scaled to match the second image. This results in \(im0”\).

The second phase correlation block is now used to find the translational offset between \(im0”\) and the second image.

It is necessary to first de-rotate and de-scale the image before finding the translational offset. This is because the recovery of translation is not invariant to rotation and scale, whereas the recovery of rotation and scale is invariant to translation.

The final result is \(im0^*\), which is the first image which has been rotated, scaled and translated to align with the second image.

[1] B. S. Reddy and B. N. Chatterji, “An FFT-based Technique for Translation, Rotation, and Scale-Invariant Image Registration,” IEEE Transactions on Image Processing, vol. 5, no. 8, pp. 1266–1271, 1996.