Rotation ambiguity

Since the magnitude plots are conjugate symmetric, there is an ambiguity in the recovered rotation. If the calculated rotation angle is \(\theta\), the actual rotation of the image could be \(\theta\) or \(\theta + \pi\). To resolve the ambiguity, Reddy et al. [1] derotate the image by both \(\theta\) and \(\theta + \pi\). Then the second phase correlation step (to recover translation) is performed on both derotated images, and the image that produces a higher peak in the inverse Fourier transform is selected. In this implementation, I assume the image is never rotated by more than 180 w.r.t the reference image, so this step is not performed. This step has been performed in imreg_dft though.

High-pass filter

Two sources of registration error are sharp boundaries (such as at the border of the images) and aliasing due to rotation [6].

Image borders

sample scene plus artifact

In the magnitude plot, there is a very obvious “plus” artifact through the centre of the image. Stone et al. [6] suggest smoothing the borders using a hanning window (also called apodization) to remove the artifact:

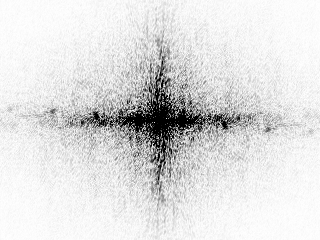
sample scene smoothed no plus artifact

Aliasing due to rotation

sample scene rotated smoothed no plus artifact

Comparing the magnitude plots of the unrotated and rotated images, some aliasing effects can be seen. During the phase correlation step, this causes false peaks at multiples of 90 degrees. Also, the peak at 0 degrees is sometimes larger than the peak at the actual rotation angle. Stone also suggests applying a high-pass filter on the magnitude plot to reduce this effect, resulting in the following magnitude plots for the unrotated and rotated images:

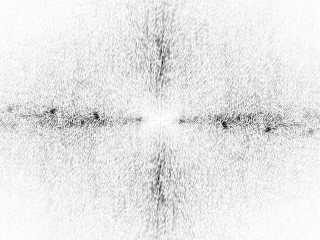
filtered 1 filtered 2

Sub-pixel registration

With the phase correlation method we are able to register two images to within a pixel since the peak is retrieved from a discrete Fourier transform. In order to register the image with sub-pixel accuracy, additional methods are required. A number of people suggest some type of interpolation around the integer-pixel peak to get a sub-pixel peak location. Examples are fitting a quadratic function around the peak (Thomas [7]), fitting a Gaussian (Abdou [8]) and fitting a sinc function (Foroosh et al. [9]). In this implementation, we calculate the centre of mass in the neighbourhood of the peak as done in imreg_dft.

[6] H. S. Stone, B. Tao, and M. McGuire, “Analysis of Image Registration Noise Due to Rotationally Dependent Aliasing,” Journal of Visual Communication and Image Representation, vol. 14, no. 2, pp. 114–135, 2003

[7] G. Thomas, “Television Motion Measurement for DATV and Other Applications,” NASA STI/Recon Technical Report N, vol. 88, p. 13496, 1987.

[8] I. E. Abdou, “Practical Approach to the Registration of Multiple Frames of Video Images,” in Electronic Imaging’99, pp. 371–382, International Society for Optics and Photonics, 1998.

[9] H. Foroosh, J. B. Zerubia, and M. Berthod, “Extension of Phase Correlation to Subpixel Registration,” IEEE transactions on image processing, vol. 11, no. 3, pp. 188–200, 2002.